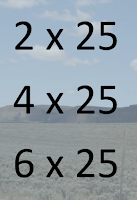Using an Open Number Line to Develop Number Sense

Take a Guess...  What readily available tool is the most UNDER-utilized mathematical tool in most classrooms? 

Did you guess the number line? If you did, you would be correct!

In our school district, a number line is one of the requirements for every mathematics classroom. In most classrooms, however, it hangs above the SmartBoard (often too high for our little learners or even for the teacher to access!) and, on most days, does little more than decorate the wall. 

Let's bring the number line to life! Cara and I created a 20-minute video that shows you 12 ways that you can use an Open Number Line in your classroom to help your students build greater Number Sense. 

VIDEO LINK: Click HERE to view the video: Using an Open Number Line to Develop Number Sense

ACTIVITY DIRECTIONS: Click HERE for a .pdf file of written directions for each activity shown in the video

NUMBER LINE MARKER CARDS: Click HERE for a copy of the number markers used for these activities - Tip: Use paper from the recycle bin. Cut the paper into strips and make number tents like the ones shown above. I find that it is actually easier this way since you don't have to hunt for the right card each time.

Number Talks: Part II

Click HERE for Number Talks: Part I (October 2016)

So you've been thinking about trying a Number Talk as part of your classroom instruction?

Okay, let's just lay it out there:

Get over your fears and all of the excuses and 

JUST GO FOR IT!

I love strategies that transcend specific topics, grade levels, or intelligences. 

That is why I am in love with Number Talks!

There are so many resources out there that can help us begin to craft our Number Talks (and if you're wondering... the Number Talk book by Sherry Parrish is a good resource, but you don't need it to run a Number Talk!).

I first posted about Number Talks in October 2016. In that earlier post, I described how to do a Number Talk and included some great links to other resources and shared a video showing a brave teacher who recorded her very first effort facilitating a Number Talk with her young students. Click HERE to see my earlier post.  

Keep reading to see more links to support using Number Talks in your classroom....

Need to be convinced even more that using a
Number Talk is a powerful teaching practice? 

• NCTM has published a set of Effective Teaching Practices. Among those practices, we can easily and strongly support at least two of them through the use of Number Talks:
• Facilitate meaningful mathematical discourse
• Elicit and use evidence of student thinking

• The Common Core Standards contain Standards of Mathematical Practices. Within these standards are three particular ones that align nicely with Number Talks:
• SMP2 - reason abstractly and quantitatively
• SMP3 - construct viable arguments and critique the reasoning of others
• SMP7 - Look for and make use of structure (Sherry Parrish says that Number Talks were specifically designed to address this one)  

• Our school district uses the PARCC Assessment to measure annual growth. Nearly 40% of the assessment asks students to Model and Reason when answering questions.  Number Talks help students learn how to reason about numbers and express their ideas clearly so others can understanding their thinking. Not just a good skill to have for testing, but a great one to have for math in the real world beyond the walls of the classroom!

• Kathy Richardson is a name we probably recognize. She is a leading contemporary in the field of mathematics education. In our school district, we use her book series Developing Number Concepts in the primary grades to support our early numeracy assessments. Take a look at what Kathy Richardson has to say about Number Talks:
  
  
  
  

• STILL not convinced? Check out this 15-minute video from Stanford University Professor Jo Boaler whose work on brain research and Growth Mindset can be seen in many schools across America!  I love how this video offers specific mathematical examples and some research to support the use of Number Talks. 

• 

  Jo Boaler, Stanford University, Number Talks
  https://www.youcubed.org/resources/stanford-onlines-learn-math-teachers-parents-number-talks/

  
  

CCPS Educators Only
Want a classroom-ready Number Talk that aligns with our CCPS Module 3? 
Look in your Module 3 Mathematics folder in Schoology

...and EVEN MORE RESOURCES (as promised)

to support your efforts to use Number Talks as a regular strategy in your classroom

PreK-Grade 5
Shametria Rout was a guest blogger on the Minds in Bloom mathematics blog and did a really nice job of addressing Number Talks in her post. Whether you are just beginning your Number Talk journey or Number Talks are already deeply embedded in your instructional repertoire, I think you will find some good stuff to add to your toolkit. Click HERE to see Shametria's post.

PreK-Kindergarten
Here is VIDEO of a Kindergarten class doing a Number Talk with Rekenreks. Even though Number Talks are typically done with no manipulatives and definitely no paper and pencil, I think you will agree that this was an effective exploration for these young learners. Click HERE for the video.

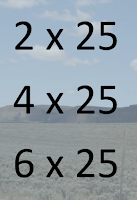
Kindergarten-Grade 5
Looking for some "ready-made" Number Talks? Then you've got to check out this S'more site created by Amy Storer. She has put together a Powerpoint collection of Number Strings that you can use with students organized by grade levels. The slides are NOT intended to be used as a presentation in one class period, but rather, plan to use just ONE SLIDE for each Number Talk and present the related equations one at a time allowing each to build on the others of the previous equation. The image to the left comes from her Grade 3-5 Multiplication series. Here, you would present just the 2x25 to kick things off (cover up the other equations). Ask students for an answer and be sure to ask "HOW DO YOU KNOW?". Be sure to solicit several different methods for determining the solution of 50. Then present the next problem 4x25 and listen for the magic of students learning to express their understanding of numbers as they explain the various ways they determined 4x25 is 100 – I think you will hear at least 3 or 4 DIFFERENT ways that students arrived at 100 if you just give students time to think and talk.  Click HERE to see 'Smore (sometimes I crack myself up!)

Kindergarten-Grade 5
As if that were not enough... here is another site with ready-made Powerpoint slides organized by grade level (K-5). Be sure to notice the grade level tabs at the top of the page. Like the previous site, these strings of expressions are not intended to be presented during one class period -- each slide is it's own Number Talk, so there is enough here to last you the entire school year! These Powerpoint slides are designed to show just one equation at a time when you play the presentation. Click HERE to see this plethora of slides you can use with your students. 

Grades 3-5
Yep, here are a few more Number Talks that you can use tomorrow in your classroom (grades 3-5). This .pdf document has dozens of examples from Sherry Parrish's book Number Talks – find the one that can help you get started in your own classroom. Click HERE to access this file. 

CRA: Concrete Representational Abstract

Perhaps the interaction above sounds familiar?
Indulge me for a moment as I ramble on like an 'Ole Timer who is reminiscing about days gone by.... 

Yes, sometimes 1/8 is greater than 1/4, but that is a discussion for another day when we chat about the importance of identifying the whole. For today, let's talk about why my students could not even answer the simple warm-up question --- and let me begin by acknowledging that I had NO ONE TO BLAME BUT MYSELF!

Do you remember that I mentioned that this was my second year of teaching? My first year was in a 1st grade classroom filled with eager six year olds and shelves full of manipulatives (or Tinker-Tools as my colleague fondly called them!). Every day, we took out the bins full of blocks and counters and soft pom poms and we used these mathematical tools to build our math understanding. Adding 7 + 4? Well, let's take out 7 blue pom poms then we'll add 4 red pom poms. If we push them all together, how many pom poms do we have now? This is what math looked like every day in 1st grade – we counted things (yes, actual things), we moved things, we stacked things, we put things side by side to compare their sizes, we weighed things, we explored math concepts. 

The next year when I changed grades and began teaching 5th grade, the blocks and counters (and most definitely the pom poms) went away and we replaced those concrete math tools with #2 pencils and eraser marks. That is why I had no one to blame but myself. 

My 5th grade students, all of 10 years old, were not quite ready to be abstract thinkers – Piaget has been telling us that for nearly 50 years! During the elementary years, children rely on their concrete experiences to develop abstract thinking because children under the age of 12 are typically still functioning in the Concrete-Operational phase of learning. Rather than dive too deeply in the Piaget pool, let's talk about this topic in more practical terms 

– let's talk about CRA. 

CRA stands for Concrete-Representational-Abstract. 
It is a three-part instructional strategy, with each part building on the previous instruction to promote student learning and retention and to address conceptual knowledge (American Institute for Research, 2016).

• During the CONCRETE phase of instruction, the students use concrete materials to explore the mathematical concepts. Counters to show a value of six. Actual containers of water to understand the concept of liquid volumes. Geoboards and rubber bands to create trapezoids and parallelograms. Attribute blocks to build an understanding of equivalent fractions.  

• Those concrete experiences can then be REPRESENTED by creating drawings, using tallies, making little circles to represent the apples in the story, or other graphical representations of the concrete model. 

• Finally, we come to ABSTRACT representations that use standard mathematical notations, such as written numbers, equal signs, and operation symbols (+ - x  ÷) to represent the problem. This phase can be used in conjunction with the Concrete and Representational phases but can only be used alone once students have a conceptual understanding of the mathematical topic.   

If I had allowed my 5th grade students to explore with these Tinker-Tools before asking, "Which is greater?", do you think any of them would have responded that 1/8 is greater? 

 (Nope, me neither)

Do you think they would have conceptually understood which was greater? 

 (Yep, me too!)

The learning progression is not a mystery.... 
In order to develop an abstract understanding of any topic, it must be rooted in a concrete experience. That is true for all of us, not just children. 

Consider this personal example: My children have seen me drive my car hundreds, no, thousands of times. But when they were old enough to drive, just seeing a representation of driving was not enough – they had to have a concrete experience of what it felt like to press the brake to truly understand just how much pressure must be applied to smoothly stop the car (and I can attest that they needed that concrete experience many, MANY times before they truly owned that knowledge!). 

So.... look around your classroom....  Do you have manipulatives that students can access? Are they hidden away in a closet? Are they only used when you decide they are needed and then under specific guidance from you? Tinker-Tools should be plentiful and accessible at all times in your classroom. A bit of warning, however, from the authors of the widely acclaimed book Teaching Student-Centered Mathematics about correctly using manipulatives in your classroom:

The most widespread error that teachers make with manipulative materials is to structure lessons in such a manner that students are being directed in exactly how to use a model, usually as a means of getting answers. There is a natural temptation to get out the materials and show children exactly how to use them. Children will blindly follow the teacher's directions, and it may even look as if they understand. A rote procedure with a model is still just that, a rote procedure.

–  Teaching Student-Centered Mathematics, Van de Walle and Lovin (2006)

   

Developing Number Sense

What a great summer! In addition to the usual summer-like activities, I also made time to enhance my own professional development. One of the areas I worked to deepen my understanding and to build my knowledge was on the topic of Number Sense. I attended more than 20 hours of webinars, facilitated a Number Sense PD opportunity at the CCPS Summer Academy, and spent time re-reading Jessica Shumway's book Number Sense Routines and John Van de Walle's book series Teaching Student-Centered Mathematics. My goal was to better understand how to help our students develop their Number Sense. Keep reading – I'd love to share what I learned with you!

What Is Number Sense? 

Number sense is NOT something that you either "have" or you "don't have". Like most things, we can cultivate our students' Number Sense. When students develop Number Sense, they understand what numbers mean, they are able to look at the world around them in terms of quantity and number (for example, they understand when 100 is a lot, and when 100 is not very much at all), and they are able to make comparisons among quantities.  

Why Is Number Sense Important?

Students who struggle in math often lack number sense. It is difficult to compute without number sense. It is a struggle to find relationships among numbers or equations without number sense. It is more arduous to figure out measurement, geometry, and data problems without number sense. In other words, number sense is the foundational building block for all strands of mathematics. As students build their number sense, mathematics takes on greater meaning. Mathematics becomes more about reaching understandings than following rigid sets of rules. With a strong number sense, children become more apt to attempt problems and make sense of the mathematics. 

 (Shumway, 2011)

Number Sense Routines in the Classroom

In Jessica Shumway's book Number Sense Routines, she reminds us that routines provide a framework for our day. Our routines help to build community and create a safe learning environment for our students. With routines, we build a sense of belonging, ownership, and predictability which makes the classroom a place to take risks, try new things, and be successful.

Number sense routines should not be "auto-pilot" activities (think about your calendar activities... would that fit into this category?). Number sense routines should be opportunities for meaningful mathematical discussions. 


Click HERE to read Math Coach's Corner on Developing FRACTION Number Sense 

             

Exactly What Is Math Fluency?

-Rethinking Fluency-

I didn't mean to do it, but I did it! I was answering a colleague's question about comprehension and fluency and found myself speaking about it as if fluency and comprehension were two different things with no connection to one another – I caught myself mid-sentence and had to readdress what I believe to be true about mathematical fluency (and how it is tightly interwoven with math comprehension).

Fluency is often described in simple terms as "fast and accurate", but there really is so much more to it than that. There are volumes of research that help us to understand the importance of developing students' conceptual understanding before beginning instruction on procedures. As we begin to build procedural fluency with students, we should continue to embed that instruction within the conceptual knowledge that students hold. 

Procedural fluency is a critical component of mathematical proficiency. Procedural fluency is the ability to apply procedures accurately, efficiently, and flexibly; to transfer procedures to different problems and contexts; to build or modify procedures from other procedures; and to recognize when one strategy or procedure is more appropriate to apply than another. To develop procedural fluency, students need experience in integrating concepts and procedures and building on familiar procedures as they create their own informal strategies and procedures. Students need opportunities to justify both informal strategies and commonly used procedures mathematically, to support and justify their choices of appropriate procedures, and to strengthen their understanding and skill through distributed practice.

~The National Council of Teachers of Mathematics (NCTM), July 2014

I can't help but notice the use of the word efficiently rather than the word fast in NCTM's position statement on fluency. Years ago, I read an article written by Linda Gojak, NCTM President (2012), where she said, "​focusing on efficiency rather than speed means valuing students’ ability to use strategic thinking to carry out a computation without being hindered by many unnecessary or confusing steps in the solution process."

Speed. How would we go about determining if something is fast? Use a timer? But how do we determine if it is fast enough? On the other hand, the term efficient needs no specific context or timer to be clearly understood. To be efficient in math, we want our students to find ways of solving problems that waste the least amount of time and effort; after all, mathematics was designed to be used as a tool to help us in our daily life, not an end unto itself. One example of how we support the notion of efficient in our county's elementary math program is by considering some of the tasks contained within our Dreambox program. Unlike many math video games, students must choose good strategies for computing answers and often are challenged to find the most efficient way to solve the problem before the game allows them to move to the next level. In our classrooms, we should be looking at these same practices to help our students strengthen their fluency skills.

- Another Way of Looking at Fluency -

At a math conference I attended a few years back, the speaker asked the room of elementary teachers to consider how we assess reading in the elementary classroom:


Think about how you assess a student’s reading ability: 

1. Do you time students to see how many words they can read correctly in a specified amount of time? (yes)
2. Do you listen and observe as students read? (yes)
3. Do you ask questions to see if students understand what they’re reading? (yes)

​
Now imagine that you ONLY used timed tests to assess reading: 

1. Do you time students to see how many words they can read correctly in a specified amount of time?

-Assessing Fluency-

Attaining fluency and assessing fluency are related, but should never be confused as being synonymous. We cannot teach students to become mathematically fluent by testing them over and over again and expecting different results each time without incorporating fluency instruction and practice that is embedded in comprehension tasks. Assessing fluency allows us to collect data that sheds light on our students' progression toward greater fluency in the Standards. As we collect this data, we should be continually creating and modifying our instructional plans to help our students attain greater mathematical fluency by deepening their understandings of the math concepts and patterns.